где Pn – частота слова с номером n, P1 – частота слова, встречающегося чаще всего.

В более общей форме закон можно записать так:

где k – некий коэффициент, а показатель степени альфа близок к единице.

При подсчете слов важно определиться, что считать словом: "наука" и "науку" – разные слова или разные формы одного слова. Если я правильно помню, в российской лингвистике были две школы, которые по-разному отвечали на этот вопрос. Как я понимаю, победила та, в которой это разные формы одного слова.

Ниже при работе с частотным словарем словом считалась только начальная форма (потому что в словаре приведены только начальные формы), при работе с прочими текстами разные формы одного и того же слова считались разными "словами" (потому что в текстах встречаются все формы).

Проверка частотного словаря русского языка

Первый, самый логичный шаг – проверить "Частотный словарь русского языка", т.к. в нем частоты уже подсчитаны.

На графике ниже представлены результаты (в двойном логарифмическом масштабе). Синим цветом показаны диаграмма рассеивания и прямая линейной регрессии, красным – прямая для "идеального" закона Ципфа.

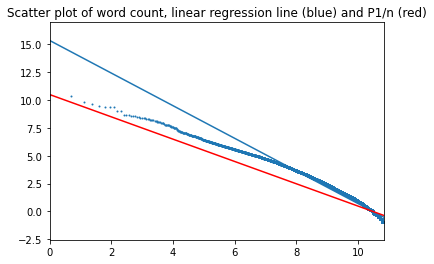
Создается впечатление, что прямая регрессии "проходит неправильно", однако это обусловлено особенностями логарифмического преобразования: точки сосредоточены в правой части графика. Левее значения 8 лежит менее 3000 точек, правее - более 49 тысяч.

P < 0.001 при R2=0.966. То есть можно сказать, что закон Ципфа довольно хорошо описывает распределение частот на всем интервале значений с показателем альфа 1,46, однако также видно, что в начале интервала – там, где расположены самые важные (наиболее часто встречающиеся) слова, – кривая отклоняется от прямой регрессии. Рассматриваю наичало интервала отдельно.

Первые три тысяч слов (5,8% от общего числа) - 75% всех употреблений.

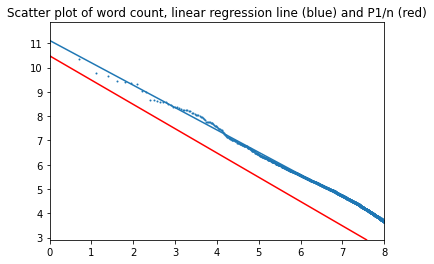
Параметры стали ближе к "идеальному" закону Ципфа. Показатель альфа 0,92. Коэффициент k 11,1. Для идеального случая k = 10,5 (доверительные интервалы и прочие параметры см. в приложенном ноутбуке).

В начало страницы

Лев Толстой. "Война и мир"

Текст книги разбит на слова и подсчитаны частоты слов.

Из всех текстов "Война и мир" ближе всего приблизилась к идеальному закону Ципфа. На два интервала график не распадается. Коэффициент наклона 0,99, свободный член 9,5 у книги, 10,2 – у идеального закона.

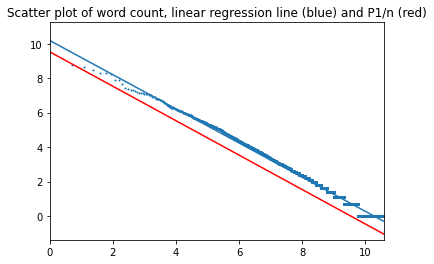
В начало страницы

Шолохов. "Тихий Дон"

Разделения на два интервала также не происходит. Коэффициент наклона 0,90, свободный член 9,9 у книги, 9,4 – у идеального закона.

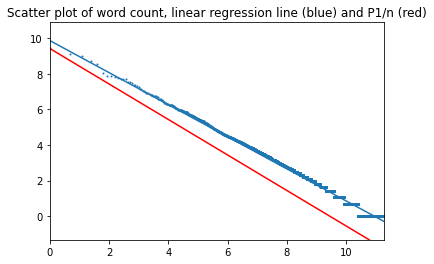
В начало страницы

Четыре романа Диккенса

«Посмертные записки Пиквикского клуба», «Жизнь и приключения Оливера Твиста», «Дэвид Копперфилд» и «Николас Никльби».

Все четыре романа были объединены в один файл, и для него был выполнен расчет частот и проверка на соответствие закону Ципфа: в трех вариантах: для оригинала на английском, для русского перевода и для машинного перевода на русский, выполненного для другого проекта.

Тексты на английском:

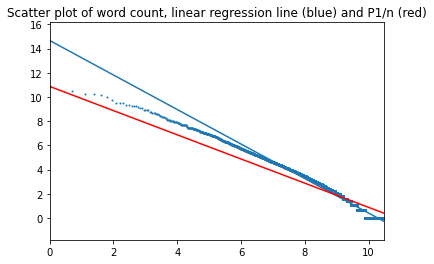
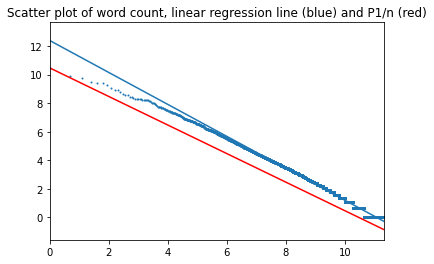
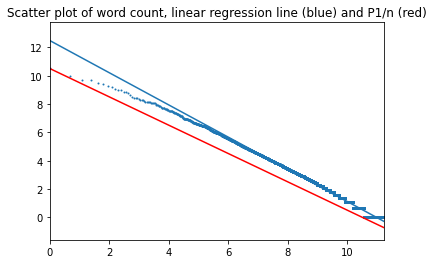
В начало страницы

Книги проекта "Гутенберг"

И наконец была выполнена проверка на нескольких сотнях книг проекта "Гутенберг", разбитых на две категории: художественная и нехудожественная литература. Все книги на английском.

Художественная литература

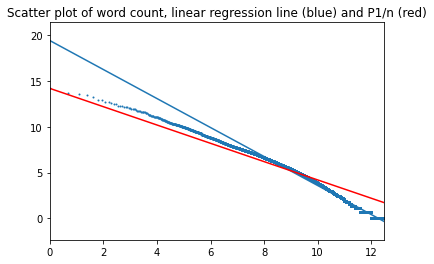
Интересно, что в данном случае прямая регрессии и линия идеального закона Ципфа пересекаются.

График для 3000 наиболее часто встречающихся слов (альфа=1,076):

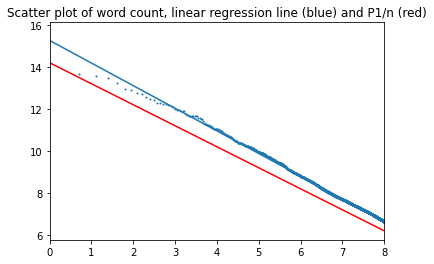
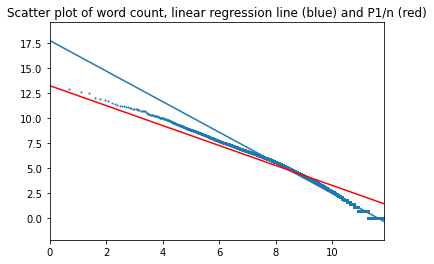
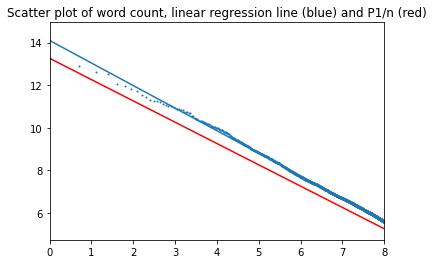
График для 3000 наиболее часто встречающихся слов (альфа=1,059):

В начало страницы