e-mail: dvkazakov @ gmail.com
(remove spaces on both sides of @)
Phone/WhatsApp: +7-916-909-7864
Telegram: @denis_v_kazakov
Skype: denis.v.kazakov
|
|
e-mail: dvkazakov @ gmail.com |
|
|
|
|
|
Checking Zipf's law validity
Skills:
Jupyter notebook of this project.
Go to conclusions
According to Zipf's law, the most frequent word in a language or a large body of texts will occur approximately twice as often as the second most frequent word, three times as often as the third most frequent word, etc. This is the "perfect" Zipf's law:
where Pn is the nth word frequency, P1 is the frequency of the most common word.
A more general form:
where k is a constant and the exponent alpha is close to unity.
To calculate frequencies, it is important to decide what a word is, e.g. are science and sciences different words or different forms of the same word? If I remember correctly, there were two schools in Russian linquistics with different answers to this question and the one that considered them to be different forms of the same word finally won.
The Frequency Dictionary of the Russian language includes only a single form of each word so there is no choice here. For other texts, I condidered different forms of the same word as different words.
Frequency Dictionary of the Russian language
The first and the most logical step is to use the Frequency Dictionary of the Russian language, as it already has word frequcencies.
Results are shown on a log-log plot below, with the scatter plot and regression line shown in blue. The red line is the "perfect" Zipf's law.
The regression line seems to be "wrong", however this is due to the nature of the logarithmic scale, as most of data points are in the right-hand side of the graph. There is less than 3000 points to the left of number 8, with over 49 thousand to the right.
P-value is less than 0.001 with R2=0.966. So it could be concluded that Zipf's law with alpha=1.46 is a good approximation of the frequency distribution over the whole range of values, however it is also quite clear that the distribution deviates from the regression line at the beginning of the range, where the most important (most frequent) words are found. So I considered the beginning of the range separately.
The first three thousand most common words (5.8% of total) accounting for 75% of all word occurences:
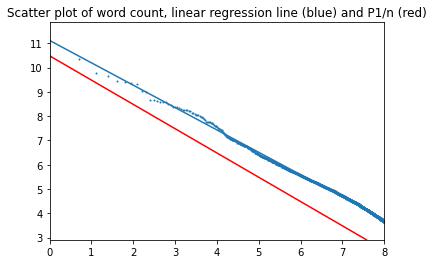
The parameters are now closer to the "perfect" Zipf's law. Alpha equals 0.92; k equals 11.1. In the perfect case, k = 10.5. (For confidence intevals and other parameters, please see the attached notebook).
Top of page
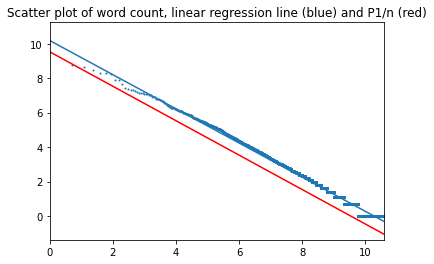
War and Peace by Leo Tolstoy
The book was split into words to calculate word frequencies.
Of all texts in this study, word frequency distributin in War and Peace is closest to the "perfect" Zipf's law. The plot does not separate into two intervals. Slope is 0.99. Intercept is 9.5 for the book and 10.02 for the perfect law.
Top of page
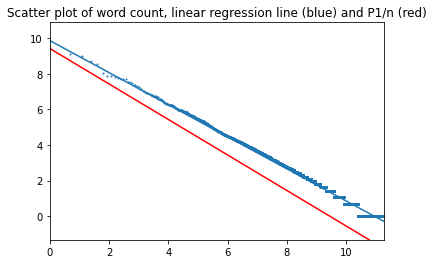
And Quiet Flows the Don by Mikhail Sholokhov
In this case, the plot also does not separate into two intervals with slope equal 0.90 and intercept equal 9.9 for the book and 9.4 for the perfect law.
Top of page
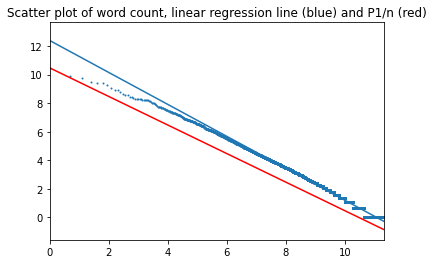
Four novels by Charles Dickens
The Pickwick Papers, Oliver Twist, David Copperfield and Nicholas Nickleby.
The four novels were merged into a single file, followed by word frequency calculation and comparison with Zipf's law. This was done for three versions: the English original, published Russian translation and a machine translation into Russian, which had been prepared for another project.
English texts:
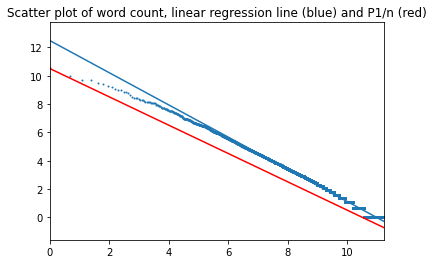
Top of page
Project Gutenberg books
Finally, I ran the same test on hundreds of books from Project Gutenberg, which were divided into two categories: fiction and non-fiction. All books were in English.
Fiction
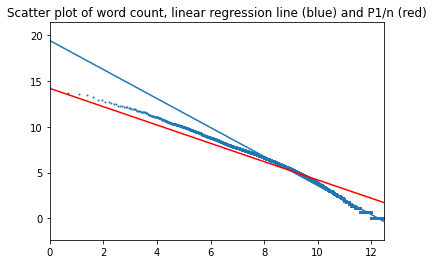
Interestingly, the regression line intersects the perfect Zipf's line in this case.
Plot for 3000 most common words (alpha=1.076):
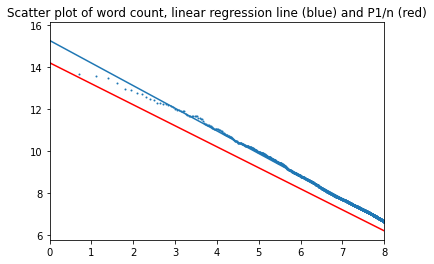
Plot for 3000 most common words (alpha=1.059):
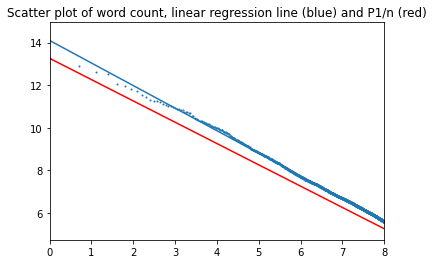
Conclusions
The generalized Zipf's law was a good approximation in all cases considered in this study. Confidence interval for alpha does not include unity (the value of alpha in the "perfect" Zipf's law).
In most cases, the distribution curve deviates from the regression line in the beginning of the interval, where the most important (most common) words are. When only the most common words are considered, Zipf's law holds but with a different exponent, closer to unity.