Прогнозирование добычи нефти и газа из нетрадиционных источников Содержание: Анализ и подготовка данных Подбор уравнения, описывающего падение добычи Прогнозирование добычи Этот проект на GitHub. Навыки: Анализ данных (EDA) Визуализация Подготовка данных (Pandas) Преобразование переменных Линейная регрессия Подбор параметров теоретических кривых (curve_fit, библиотека Scypy) Временные ряды Нейронная сеть (keras, functional API) Подбор метрик с учетом отраслевых требований Изучение предмета анализа (разработка сланцевых местрождений) Источник данных: Общество инженеров-нефтяников (SPE).

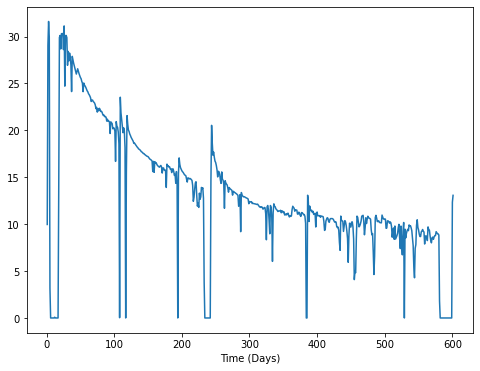
Дебит (количество нефти или газа, добываемое за сутки) скважин, пробуренных на сланцевые пласты, со временем обычно снижается. Для определения экономических показателей важно прогнозировать скорость падения и общий объем, который будет добыт из скважины.

Анализ данных

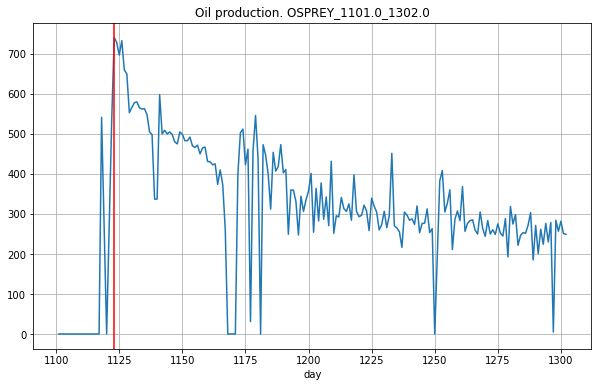
Всего есть данные по 53 скважинам, из них 11 нефтяные, остальные газовые. Кроме того, во всех скважинах было обводнение продукции. Данные сложные, в конструкцию многих скважин несколько раз вносили изменения, что меняло форму кривой, были простои, когда добычи не было. Кроме того, в начале эксплуатации есть период неустановившегося притока с хаотичным изменением дебита. (Красные вертикальные линии – даты внесения изменений.)

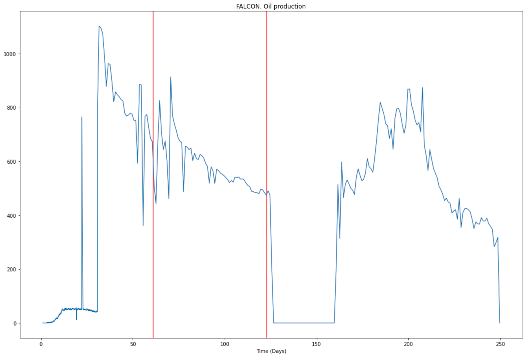
Также есть геологическая информация, данные по конструкции скважин.

Во всех скважинах, даваших нефть, применялся газлифт, но не постоянно.

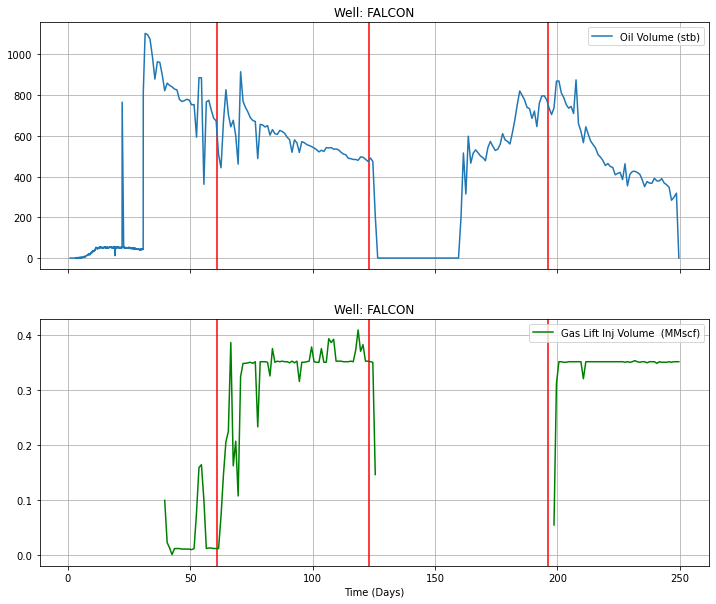
Подготовка данных

Выявил точки изменения режима. Отделил данные по добыче нефти от данных по добыче газа. Удалил периоды неустановившегося притока. Разбил данные на временные интервалы с более-менее постоянным режимом. Преобразовал переменные, чтобы можно было использовать (как один из вариантов) линейную регрессию. Ниже красным отделен нестабильный интервал.

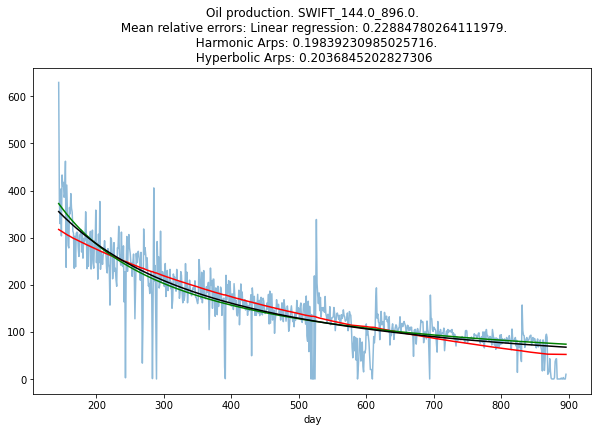
Проверка выполнения закона Арпса

По сути, это отдельный проект. Для описания снижения дебита часто использую закон Арпса, который существует в трех вариантах: экспоненциальном, гармоническом и гиперболическом. Цель проекта – выяснить, можно ли использовать его в данном случае.

Попробовал несколько способов.

Два варианта для экспоненциального закона: преобразование переменных под линейную регрессию и прямой подбор кривой с помощью функции curve_fit из библиотеки SciPy. Для двух других уравнений - только подбор кривых.

Поскольку все временные интервалы и скважины разные для сравнения использовал среднюю относительную ошибку (mean absolute percentage error, библиотека scikit-learn).

Результаты разных методов похожие, но линейная регрессия и приближение с помощью экспоненциального закона иногда дают очень большую ошибку. Гиперболическое и гармоническое приближение работают довольно хорошо, учитывая простую модель и ограниченный набор данных.

Прогнозирование добычи

На вход модели поступают данные с разной размерностью: данные по скважинам и геологические данные - одномерные, объемы добычи нефти, газа и воды - двумерные, т.к. для обучения использовал начальный период добычи, т.е. эти данные зависят от времени.

Попробовал несколько вариантов архитектуры нейронной сети с использованием LSTM и без него. Выборка нефтяных скважин маленькая - 22 кривые, поэтому как тестовую использовал всего одну. Результаты обучения нейросети нестабильный (повторный запуск обучения дает другой прогноза), сеть склонна к переобучению. Относительная ошибка на тестовой скважине ~60%.

Газовых скважин больше - 53 кривые (50 в выборке для обучения, 3 тестовые). Добавил регуляризацию (dropout). Результаты улучшились. Если использовать для обучения первые 60 дней добычи, относительная ошибка на тестовой выборке 20-25%. Хотя проблемы с переобучением и нестабильностью остаются.

Следущий шаг - попробовать совместить нейронную сеть с подгонкой кривых, т.к. в целом дебит подчиняется закону Арпса. Или найти набор данных побольше.

Пример архитектуры нейронной сети: